ひずみとは？単位は？わかりやすく解説します

物体が荷重を受けると、物体には「ひずみ」が生じます。

この「ひずみ」は、材料力学の教科書に必ずのっている用語です。

ただ、教科書だと紙面の都合で解説や図が少なかったり、説明が堅苦しすぎたりして理解が難しいと感じる人もいるでしょう。

そこで本記事では、工学的な要素はおさえつつも、できるだけわかりやすく「ひずみ」について解説したいと思います。

ひずみの漢字と英語

ひずみは漢字では「歪、もしくは歪み」と書きます。

工学分野の話をするときは「ゆがみ」とは言わないので、注意しましょう。

英語では「strain」と言います。

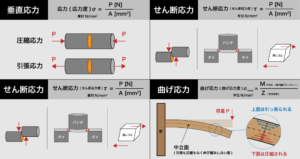
縦ひずみとは?

引張ひずみとは?

例えば、上図のような丸棒があったとします。

この棒を引っ張ると、少し伸びてちょっと細くなることは、なんとなくイメージできるかと思います。

この伸び率(変化率)の事を「ひずみ」と言います。

また、上図のように荷重方向のひずみの事は、より細分化して「縦ひずみ」と言います。

縦ひずみの中でも上図は引張方向のひずみですので、さらに細分化して「引張ひずみ」ということもあります。

引張ひずみの公式・計算式

引張ひずみの計算式は上図の通り「ε = λ/l」となります。

εはイプシロン、λはラムダと読みます。

ひずみの分母には「棒の元の長さ」、分子には「伸びた量」がきます。

つまり、ひずみというのは伸びた絶対量の事ではなく「元の長さに対してどれくらい伸びたか、という変化の比率」を表しています。

後ほど詳しく書きますが、ひずみは「物体がどのくらい伸びたり縮んだりしたかという比率の事」を言うので、単位はありません。

伸びた絶対量と勘違いし、mmやmなどの単位があると間違えないようにしましょう。

圧縮ひずみとは?

先ほどは棒の引張方向に荷重がかかっていました。

今度は圧縮方向に荷重がかかっているパターンを考えてみます。

上図の丸棒を潰すように圧縮方向に荷重をかけると、棒の長さは縮み、太さは太くなるイメージはできるかと思います。

この圧縮方向に荷重がかかる時のひずみの事を「圧縮ひずみ」と言います。

圧縮ひずみの公式・計算式

圧縮ひずみの計算式は、上図の通り「ε = λ/l」となります。

引張ひずみの時と、公式自体は同じです。

しかし、変化量のλは引張方向をプラス(正)と考えますので、圧縮ひずみの場合のλはマイナス（負)となります。

分母の元の棒の長さはもちろんプラス(正の値)ですから、圧縮ひずみεは、マイナス(負の値)となります。

ひずみの単位

縦ひずみの公式からわかるとおり、ひずみの分母には「物体の元の長さ」、分子には「変化量」がきます。

つまり、ひずみというのは伸びた絶対量の事ではなく「元の長さに対してどれくらい伸びたか、という変化の比率」を表しています。

よって、ひずみの単位は無次元(なし)になります。

縦ひずみにはプラスマイナス(正負)があり、引張方向はプラス(正)、圧縮方向はマイナス(負)になります。

横ひずみとは?

感の良い方はもうわかったかもしれませんが、縦ひずみがあれば横ひずみもあります。

横ひずみは、荷重方向と垂直方向のひずみの事を言います。

公式の概念自体は縦ひずみと同じです。

縦ひずみと同様、横ひずみも分母に「元の物体の大きさ」、分子に「変化量」がきます。

上図は、引張荷重を受けた時の横ひずみの図です。

縦ひずみがプラス(正)の時、横ひずみはマイナス(負)となるので、上図の横ひずみはマイナスの値となります。

ひずみの符号(プラスマイナス)

	縦ひずみ(ε,λ)	横ひずみ(ε′,δ)
引張荷重	+	–
圧縮荷重	–	+

縦ひずみ、横ひずみの符号はまとめると上記の通りとなります。

各方向、でかくなる方向(変形量がプラスの方向)がそのままプラスになると覚えるとわかりやすいでしょう。

垂直ひずみとは?

縦ひずみと横ひずみは、どちらも垂直方向の荷重により発生します。

よって、「縦ひずみ」と「横ひずみ」の2つを総称して「垂直ひずみ」と呼びます。

これはただの用語定義ですので「そういう風にまとめて呼ぶ事もあるのだ」くらいに考えておけば良いでしょう。

ひずみの記号の読み方は？【ギリシャ文字のε(イプシロン)です】

ひずみの式に出てくる記号は、ギリシャ文字のε(読み：イプシロン）です。

ひずみとは？単位は？わかりやすく解説します【まとめ】

今回は、できるだけわかりやすくひずみについて解説してみました。

理解の助けになれば嬉しく思います。