物体が外から力を受けた時、物体の内部に発生する力の事を応力(おうりょく)と言います。
英語ではStressと言います。
材料力学を勉強する上でこの「応力」を理解する事は大切です。
言葉だけだと良くわからないと思いますので、具体的なイラストを交えてわかりやすく解説していきたいと思います。
応力とは

例えば、上図のように外力Pで引っ張られている棒があったとします。
この力に抵抗する力が無い場合、棒はびよーんと伸びてしまうはずです。
しかし今回、棒は見た目の上では形状を保っています。
つまり「棒の内部には外力による変形に抵抗する力、外力に応じる力」が働いている事になります。
この変形に抵抗する力、外力に応じる力の事を「内力、もしくは応力」といいます。
単位は力の単位であるN(ニュートン)になります。

より深く理解するために、仮想の断面Aで切断して考えてみます。
外力Pとつりあうために、棒の断面Aには内力Qが発生します。
つまり、棒の内部にこの外力に抵抗する力である応力が発生しているため、棒は形状を保っていられることになります。
応力度とは?

単位面積あたりの内力を応力度といいます。
単位面積当たりの力ですので、単位は「N/mm^2」や「N/m^2」になります。
機械系では、この応力度の事を単に応力としている事が多いです。
当記事では、単位面積あたりで割った応力の事を言うときは「応力(応力度)」とかっこ書きして、単位面積で割った応力(つまり応力度)の事を言っているのだとわかるようにしておきたいと思います。
応力(応力度)を計算する

- 外力P:1000 N
- 棒の断面積A: 100 mm^2
上記の場合の応力(応力度)σを計算したいと思います。
棒の断面積をA(mm^2)とすると、応力(応力度)σは下記の式で表されます。
よって
σ = 10 [N/mm^2]
となります。
この応力(応力度)が、材料の耐えられる範囲を超えると破壊に至ります。
応力(応力度)は外力と断面積で決まる
応力(応力度) = 外力/断面積
上記式を見ればわかりますが、応力(応力度)は断面積と外力で決まります。

断面積が小さくなると、応力(応力度)は大きくなります。
例えば、外力が一定の場合、上記のように断面積が4分の1になると、応力(応力度)は4倍になります。

外力が大きくなると、応力(応力度)は大きくなります。
例えば、断面積が一定で外力が2倍になると、応力(応力度)も2倍になります。
設計観点でざっくり言うならば、
- 部品にかかる外力を小さくする
- 部品の断面積を大きくする
という事をすれば、物体は破壊されにくくなると言えます。
逆に、もし応力(応力度)に余裕がある場合は、部品の断面積を小さくして小型化、軽量化を測る余地があるとも言えます。
応力の種類
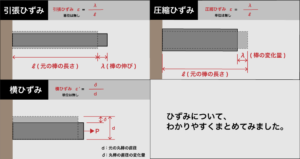
- 引張応力(引張応力度)
- 圧縮応力(圧縮応力度)
- せん断応力(せん断応力度)
- 曲げ応力(曲げ応力度)
応力(応力度)には、上記のような種類があります。
引張応力(引張応力度)と圧縮応力(圧縮応力度)は、合わせて垂直応力(垂直応力度)と言います。
垂直応力(引張応力、圧縮応力)とは

部材の断面に対しての垂直方向の応力を垂直応力(垂直応力度)と言います。
部材を引っ張る方向は引張応力(引張応力度)、押し縮める方向の場合は圧縮応力(圧縮応力度)と言います。
せん断応力とは

断面に平行な方向に働く応力のことをせん断応力(せん断応力度)と言います。
断面をずらす、切断するような方向を考えれば良いです。
上図のようなイメージです。
曲げ応力とは

壁からはり(角棒)が生えていて、荷重Pにより曲がっているとします。
この場合、材料の上面側は伸びる事になるので、引張応力が発生します。
反対に、材料の下面側は縮む事になるので、圧縮応力が発生します。
これらの引張応力や圧縮応力は曲げが起きた時に発生する応力です。
まとめて「曲げ応力(曲げ応力度)」と言います。
応力とは?【まとめ】
- 物体が外から力を受けた時、物体の内部に発生する力の事を応力と言う
- 応力の単位は力の単位であるN(ニュートン)
- 応力を単位面積で割ったものを応力度と言う。機械系の材料力学では、単に応力と言えば面積で割った応力度の事を指す事が多い
- 応力には【引張応力】【圧縮応力】【せん断応力】【曲げ応力】といった種類がある
以上、応力(応力度)に関する基本の解説でした。



コメント